Эффективная ставка (доходность) по вкладу
Эффективная ставка по вкладу отличается от номинальной только в случае капитализации процентов, и рассчитывается в зависимости от частоты капитализации и срока вклада. Среднее увеличение процентной ставки происходит на 0,1 — 0,5 процента.
Уже давно вклад денег в банк стал одним из способов заработать благодаря доходам от дивидендов. Считается, что это самый безопасный способ извлечения выгоды благодаря финансовым манипуляциям собственными средствами — деньги вкладываете вы, а их оборотом и начислением процентов занимается профессиональная организация, банк. В большинстве случаев, клиентам озвучивается номинальная ставка, что далеко не действительно отражает весь потенциальный доход по вкладам. Его отражает эффективная ставка.
Что такое эффективная ставка по вкладу
Эффективная ставка – это коэффициент, который используется в расчете настоящего дохода от вложения денежных средств на банковский депозит. Она характеризуется учетом капитализации процентов и всегда превышает показатели номинальной ставки. Это объясняется тем, что проценты по капитализации рассчитываются с учетом заданной периодичности и прибавляются к телу депозита.
Она характеризуется учетом капитализации процентов и всегда превышает показатели номинальной ставки. Это объясняется тем, что проценты по капитализации рассчитываются с учетом заданной периодичности и прибавляются к телу депозита.
Зачем нужно знать эффективную ставку
Эффективная процентная ставка используется для определения всего дохода за срок депозита с учетом процентов. Зная этот показатель, клиент может реально оценить свой возможный доход и целесообразность вложения средств на заданных условиях. Стоит отметить, что для достижения максимального дохода от вкладов следует отдать предпочтением тем, у которых капитализация процентов ежемесячная.
Система работает таким образом, что в первый месяц работы вклада проценты прибавляются к телу. На второй и последующие месяцы проценты будут начисляться на сумму, которая состоит из тела депозита и дивидендов за предыдущий месяц. В итоге получается, что общий доход по депозиту превышает исходный показатель ставки.
Формула расчета
Для того чтобы произвести расчет эффективной процентной ставки, применяется формула сложных процентов, которая имеет следующее выражение:
ЕС = ((1*(С/100)/N)N*m −1),
где ЕС – эффективная ставка по вкладу, то есть доход, который вы получите по окончании срока;
С – обозначение номинальной ставки, которая обычно указана в договоре;
N – обозначение интервалов капитализации относительно ее периодичности;
m – количество повторений интервалов.
Влияние пополнения или частичного снятия на эффективную ставку
При изменении размера тела депозита, соответственно, происходит изменение дивидендов по вкладу – чем больше размер вклада, тем больше клиент сможет заработать процентов, при уменьшении тела депозита действует эта же закономерность.
Расчетформула эффективной ставки помогает вкладчикам ориентироваться в рентабельности вкладов относительно потенциально получаемых процентов, что чрезвычайно удобно. Также клиент сам может выбирать удовлетворяющие его те или иные условия по вкладам касательно сроков вложения средств.
Также клиент сам может выбирать удовлетворяющие его те или иные условия по вкладам касательно сроков вложения средств.
Правда и мифы о деньгах в Facebook
Подписаться
Статья была полезной?
204 113
Комментировать
Рекомендуемые вклады
Вклад "Мёд"
Срок
от 182 дней до 1098 дней
Выгодный вклад с доходностью до 7,04% годовых.
Срок
от 3 месяцев до 2 лет
Банки начали повышать ставки по вкладам после решения ЦБ — Frank RG
Ставки поднял Альфа-Банк
pixabay
Банки начали повышать ставки по рублевым депозитам, показал мониторинг тарифов Frank RG. ЦБ повысил ключевую ставку до 4,5%, а банкиры прогнозировали, что ставки по кредитам и вкладам также изменятся.
Детали. В понедельник, 22 марта, сразу несколько банков повысили ставки по вкладам. Альфа-Банк поднял эффективную ставку по Альфа-Вкладу сроком на 3 года на 0,69 п.п., до 6% годовых.
Банк Авангард повысил ставки по вкладам на 0,2 п. п. Максимальная ставка по депозитам «Базовый» и «Базовый-Интернет» выросла до 4% годовых. Максимальные ставки увеличились на 0,25 п.п. в банке Санкт-Петербург — по вкладам «Управляемый» и «Управляемый online». Самая высокая ставка по депозиту «Управляемый online» достигла 2,5%.
п. Максимальная ставка по депозитам «Базовый» и «Базовый-Интернет» выросла до 4% годовых. Максимальные ставки увеличились на 0,25 п.п. в банке Санкт-Петербург — по вкладам «Управляемый» и «Управляемый online». Самая высокая ставка по депозиту «Управляемый online» достигла 2,5%.
Максимальная ставка по вкладу «Управляемый» банка Кубань Кредит выросла на 0,13 п.п. до 2,25%. Диапазон ставок по депозиту «Гарант» в Реалист Банке увеличился на 0,25 п.п. до 5,05-5,15%. СДМ-Банк повысил ставки по вкладам «Детский» и «Пенсионный» на 1,75 п.п. до 5%.
Индекс банковских ставок FRG100 на 22 марта составил 4,1018%. Индекс растет с ноября прошлого года, за неделю он прибавил 349 пунктов.
Статистика по теме
На рост ключевой ставки отреагировали также ставки по ипотечным кредитам. С 22 марта на 0,25 п.п. выросли максимальные ставки по отдельным продуктам у Совкомбанка, банка Дом.РФ, ТКБ, Уралсиба, ЮниКредит Банка и Открытия.
Мнение эксперта. Управляющий директор рейтингового агентства НКР Станислав Волков полагает, что значительного риска попасть в «процентные ножницы» у банков нет. «Мы не ожидаем существенного снижения процентной маржи банков в 2021 году, так как у них есть возможность сдерживать рост доходности по депозитам», — рассказывает он. Поскольку у вкладчиков стали востребованными накопительные счета, многие клиенты не будут спешить переводить средства на вклады, даже если их доходность вырастет на несколько десятых процента, поясняет Волков. «Незначительное снижение маржи банки смогут компенсировать за счёт роста кредитного портфеля», — заключает эксперт.
Управляющий директор рейтингового агентства НКР Станислав Волков полагает, что значительного риска попасть в «процентные ножницы» у банков нет. «Мы не ожидаем существенного снижения процентной маржи банков в 2021 году, так как у них есть возможность сдерживать рост доходности по депозитам», — рассказывает он. Поскольку у вкладчиков стали востребованными накопительные счета, многие клиенты не будут спешить переводить средства на вклады, даже если их доходность вырастет на несколько десятых процента, поясняет Волков. «Незначительное снижение маржи банки смогут компенсировать за счёт роста кредитного портфеля», — заключает эксперт.
Контекст. В пятницу, 19 марта, ЦБ повысил ключевую ставку на 0,25 п.п. до 4,5%. Свое решение регулятор объяснил быстрым ростом инфляции. В феврале инфляция увеличилась до 5,7% после 5,2% в январе, а по оценкам на 15 марта, она составила 5,8%. «Показатели, отражающие наиболее устойчивые процессы ценовой динамики, по оценкам Банка России, находятся значимо выше 4% в годовом выражении», — подчеркивал ЦБ в пресс-релизе.
По словам банкиров, повышение ставки отразится на доходности вкладов, а также на стоимости кредитов. «Рост ключевой ставки на 0,25 п.п. на данный момент не вполне заложен банками в текущие кредитные и депозитные ставки. Поэтому возможен рост ставок по всем банковским продуктам (как в части кредитования, так и размещения средств)», — отмечал руководитель казначейства Альфа-Банка Артем Павлов. Старший экономист аналитического управления «Открытие Research» банка Открытие Максим Петроневич писал в комментарии, что рост ключевой ставки будет трансформироваться в рост ставки по депозитам, прежде всего наиболее популярной срочности: от полугода до года и чуть больше года.
Зачем вам об этом знать. Рост ставок по вкладам может привести к снижению маржи банков из-за большого объема кредитов, выданных ранее под низкие ставки. Однако, маловероятно, что финансовое положение банков существенно ухудшится.
Во времена финансовых кризисов банкирам важно оставаться в курсе текущих новостей. Подпишись на наш телеграм – канал Frank RG (https://t.me/frank_rg) чтобы оперативно получать данные о ситуации в банках и экономике. Не пропусти, когда начнется!
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Какой должна быть разумная ставка по кредиту?
Волна потребительского кредитования захлестнула Россию — этот, в недавнем прошлом для многих экзотический, способ решать свои имущественные проблемы сейчас стал повсеместным. Как обычно бывает в России, процесс пошел с «перехлестом» в обратную сторону: граждане стали набирать кредитов, не особо задумываясь о том, каким образом будут их возвращать. При этом российское кредитование, в очень серьезной мере, все еще находится в полосе «дикой» экономики, поэтому ставки кредитования часто никак не сообразуются не только с экономической ситуацией, но и просто со здравым смыслом. Какой должна быть разумная ставка по кредиту — об этом мы спросили у законодателей.
Какой должна быть разумная ставка по кредиту — об этом мы спросили у законодателей.
Вопрос недели: Какой должна быть разумная ставка по кредиту?
Ольга Баталина, первый заместитель председателя Комитета Государственной Думы по вопросам семьи, женщин и детей, фракция «Единая Россия»:
— Мировой опыт потребительского кредитования показывает, что ставки по потребительским кредитам колеблются от 8 до 12 процентов. Считаю, что в случае, если это эффективная процентная ставка, включающая иные платежи по кредиту, то это разумный подход. Когда мы анализируем размер процентной ставки, нужно понимать, что проценты — это не единственное направление расходов физического лица по обслуживанию кредитов. Очень важно при заключении кредитного договора рассчитывать эффективную процентную ставку — фактическую сумму средств, которую гражданин должен будет ежемесячно выплачивать банку.
Николай Панков, председатель Комитета Государственной Думы по аграрным вопросам, фракция «Единая Россия»:
— Для аграриев было бы неплохо установить процентную ставку в 8 процентов. Есть государства, где сельхозкредиты дают под 2-4 процента. Сейчас Министерство сельского хозяйства компенсирует банкам процентную ставку по кредитам сельхозпроизводителям. Но аграрии не просят компенсации — им нужны доступные кредиты. Пока же процентная ставка для них — 14-15 процентов. Банки мотивируют завышение процентных ставок недостаточной налоговой базой, просчитывают риски, и в итоге кредиты дорожают.
Есть государства, где сельхозкредиты дают под 2-4 процента. Сейчас Министерство сельского хозяйства компенсирует банкам процентную ставку по кредитам сельхозпроизводителям. Но аграрии не просят компенсации — им нужны доступные кредиты. Пока же процентная ставка для них — 14-15 процентов. Банки мотивируют завышение процентных ставок недостаточной налоговой базой, просчитывают риски, и в итоге кредиты дорожают.
Елена Панина, член Комитета Государственной Думы по экономической политике, инновационному развитию и предпринимательству, фракция «Единая Россия»:
— С точки зрения потребителя, идеальной будет нулевая ставка по кредиту. Но это шутка. Считаю, разумной будет ставка не больше 2 процентов. Но у нас другая кредитная система. В России корпоративные кредиты хорошим, надёжным заёмщикам идут под 12-13 процентов годовых, а остальным — под 15 процентов. Так что и ставка для потребительских кредитов не может быть намного ниже. Чтобы снизить ставки, кредитная система должна быть в целом другой. Но на процентную ставку влияют и другие факторы — например, инфляция. И самое главное в том, что в России нет конкуренции коммерческим кредитам, как в других странах. За границей есть ставка рефинансирования, и можно перекредитоваться по другим ставкам, в том числе взять кредит у государства. Таким образом там регулируется рынок кредитования.
Но на процентную ставку влияют и другие факторы — например, инфляция. И самое главное в том, что в России нет конкуренции коммерческим кредитам, как в других странах. За границей есть ставка рефинансирования, и можно перекредитоваться по другим ставкам, в том числе взять кредит у государства. Таким образом там регулируется рынок кредитования.
Валерий Рязанский, председатель Комитета Совета Федерации по социальной политике:
— Вообще ставки по кредитам в России разорительны. Но лично меня, как гражданина, из всех видов кредитования больше всего тревожит высокий уровень процентных ставок по ипотеке. Получается, что вся кредитная политика работает не на интересы людей, а на интересы финансовых институтов.
Вячеслав Новиков, заместитель председателя Комитета Совета Федерации по бюджету и финансовым рынкам:
— Процентная ставка зависит от уровня рентабельности основного производства. То есть, если предприниматель берёт кредит, то он должен знать, что получит хоть какую-то прибыль. Я думаю, ставка для малого бизнеса не должна превышать 10 процентов, это оживит российскую экономику, хотя и эти цифры — выше, чем на Западе. Если же говорить о потребительских кредитах населению, то ставка не должна превышать 12 процентов. Но при этом точно должны быть известны доходы каждого заёмщика, его кредитная история и тот факт, что он максимально благонадёжен. А то наши банки завышают процентную ставку и за счёт этого компенсируют убытки, которые несут из-за недобросовестных заёмщиков.
Я думаю, ставка для малого бизнеса не должна превышать 10 процентов, это оживит российскую экономику, хотя и эти цифры — выше, чем на Западе. Если же говорить о потребительских кредитах населению, то ставка не должна превышать 12 процентов. Но при этом точно должны быть известны доходы каждого заёмщика, его кредитная история и тот факт, что он максимально благонадёжен. А то наши банки завышают процентную ставку и за счёт этого компенсируют убытки, которые несут из-за недобросовестных заёмщиков.
Дмитрий Вяткин, заместитель председателя Комитета Госдумы по конституционному законодательству и государственному строительству, фракция «Единая Россия»:
— Ставка потребительских кредитов определяется не соображениями разумности, а экономическими соображениями. Когда говорят о том, что нужно снизить нормативным путём учётную ставку Центробанка и тем самым подтолкнуть коммерческие банки к снижению ставок по кредитам — это не выход, потому что будет соответственно снижена ставка по вкладам. Здесь существует прямая связь. Снизится ставка по вкладам — значит люди перестанут нести деньги в банк и соответственно кредитоваться будет нечем.
Здесь существует прямая связь. Снизится ставка по вкладам — значит люди перестанут нести деньги в банк и соответственно кредитоваться будет нечем.
Оксана Дмитриева, первый заместитель председателя Комитета Госдумы по бюджету и налогам, фракция «Справедливая Россия»:
— В данном случае вопрос о разумности не стоит. Потому что ставка по кредиту всегда должна превышать уровень инфляции. Ведь всё зависит от круговорота денег в стране. Например, если у нас инфляция 6 процентов, то рублёвая кредитная ставка может быть в районе 7 процентов.
Подготовили: Мария Соколова, Ксения Редичкина
Процентная ставка (percent rate) — Финансовый журнал ForTrader.org
Процентная ставка — что это?
Процентная ставка (англ. percent rate) – это процент, который взимается кредитором за пользование заемными средствами. Расчетный период ставки бывает различным и устанавливается в договоре отдельно, обычно это месяц, квартал или год.
Какие бывают процентные ставки?
Выделяют:
- процентные ставки Центробанка,
- ссудных операций кредитных институтов с небанковскими клиентами,
- доходности ценных бумаг (например, облигаций)
- и т.д.
Процентная ставка может быть реальной, т.е. очищенной от инфляции, или номинальной, которая учитывает размер инфляции. Также выделяют фиксированные ставки, которые не изменяются на всем протяжении договора, и плавающие процентные ставки, которые пересматриваются раз в определенный период. К последним, к примеру, относится процентная ставка LIBOR (Лондонская межбанковская ставка предложения).
На что влияет процентная ставка в экономике?
Уровень процентной ставки, устанавливаемый Центробанком, является важным показателем экономической стабильности страны, т.к. является инструментом монетарной политики. Чем она выше, тем выше инвестиционный интерес иностранных вкладчиков и больше их вклады в национальную экономику. Для внутренней экономики высокая процентная ставка – это сокращение сумм кредита, что не всегда хорошо влияет на развитие, однако замедляет инфляционные процессы.
Для внутренней экономики высокая процентная ставка – это сокращение сумм кредита, что не всегда хорошо влияет на развитие, однако замедляет инфляционные процессы.
Как процентные ставки влияют на рынок Форекс?
Разница между процентными ставками Центральных Банков (процентный дифференциал) выполняет ключевую роль в формировании обменного валютного курса. Повышение ставки расценивается инвесторами как возможность получения безрискового дохода и вызывает увеличенный спрос на национальную валюту. Понижение наоборот – причина оттока капитала из экономики государства и, как следствие, ослабляет национальную валюту.
В современных условиях Центробанками для воздействия на курс национальной валюты (наряду с валютными интервенциями) широко применяется метод регулирования процентными ставками. Видов процентных ставок много, но для валютного рынке наиболее интересны официальная и банковская процентные ставки.
Официальная процентная ставка – это ставка, под которую коммерческие банки занимают деньги у центрального банка.
Банковская процентная ставка – это размер платы банку за пользование денежной ссудой, выраженный в процентах.
Все виды ставок связаны между собой и определяются официальной, которую устанавливают Центробанки в своих странах.
- Уменьшение процентных ставок приводит к увеличению деловой активности и увеличивает инфляцию, курс национальной валюты при этом понижается.
- Увеличение процентных ставок в свою очередь, наоборот, приводит к снижению деловой активности, снижению инфляции и повышению курса.
Из-за того, что есть такая взаимосвязь мы имеем следующую закономерность: чем больше официальная процентная ставка в каком–то государстве, тем больше желающих купить валюту этой страны, чтобы разместить средства в депозит под более высокую ставку, и значит курс этой валюты растет.
Например, на конец 2015 года, процентная ставка ФРС составляла 0,25% с перспективой ее увеличения, а у ЕЦБ была 0,05% с перспективой дальнейшего ослабления кредитно-денежной политики, что стало причиной длительного падения валютной пары EUR/USD.
В зависимости от особенностей государственной экономики, ЦБ, изменяя уровень процентной ставки, выполняют функции регулирования инфляции, дефляции, поддержки или замедления экономического роста.
Результаты заседаний ЦБ по кредитно-денежной политике, на которых принимаются решения по размеру процентной ставки, являются важнейшими событиями экономического календаря и вызывают повышенную волатильность на Форекс в соответствующих валютных парах.
Процентные ставки крупнейших мировых Центробанков
- ФРС США – Target Fed Fund Rate. Основную процентную ставку в США устанавливает Федеральный Комитет по Открытым Рынкам (FOMC – Federal Open Market Committee). Она носит название «целевой ставки по федеральным фондам» (Target Fed Fund Rate) и является основной мировой процентной ставкой.
- ЕЦБ – Refinancing tender. Является аналогом американской Target Fed Fund Rate. Европейская ставка рефинансирования является минимально возможной ставкой по заявкам на привлечение средств в рамках тендера ЕЦБ.
 Каждые две недели, с целью поддержать ликвидность в финансовой системе, европейский регулятор проводит тендер по размещению средств. То есть, по сути, это минимальная ставка, по которой проходит совершение сделок ЕЦБ на открытом рынке. Refinancing tender является второй по значимости процентной ставкой в мире.
Каждые две недели, с целью поддержать ликвидность в финансовой системе, европейский регулятор проводит тендер по размещению средств. То есть, по сути, это минимальная ставка, по которой проходит совершение сделок ЕЦБ на открытом рынке. Refinancing tender является второй по значимости процентной ставкой в мире. - Банк Англии – Repo rate. Является процентной ставкой, под которую Банк Англии выдает британским банкам краткосрочные ссуды, залогом по которым являются ценные бумаги. Банки обязуются выкупить свои активы через определенный срок по определенной цене.
- Швейцарский Национальный Банк – Libor Rate. Целевая трехмесячная ставка Libor используется Швейцарским Национальным Банком как инструмент для регулировки кредитно-денежной политики. Оно является серединой двухпроцентного диапазона. Также она носит название исходной ставки, посредством которой ШНБ оказывает влияние на проценты по ссудам, сбережениям и ипотеке.
- Центральный Банк Японии – Overnight call rate target.
 Является аналогом американской Target Fed Fund Rate. Процентная ставка Банка Японии является для него ориентиром в качестве среднего значения на рынке краткосрочных вкладов. Чтобы приблизить процентные ставки по банковским депозитам к целевому значению, Банк Японии манипулирует государственными ценными бумагами.
Является аналогом американской Target Fed Fund Rate. Процентная ставка Банка Японии является для него ориентиром в качестве среднего значения на рынке краткосрочных вкладов. Чтобы приблизить процентные ставки по банковским депозитам к целевому значению, Банк Японии манипулирует государственными ценными бумагами. - Центробанк Канады – Overnight rate target. Целевая ставка Банка Канады Overnight rate target является ориентиром по займам для банков и финансовых организаций. Посредством ее изменения канадский регулятор оказывает влияние на банковские ссуды, кредиты, сбережения и объемы ипотечного кредитования.
- Резервный Банк Австралии – Official Cash rate. Процентная ставка РБА – это ставка по межбанковским краткосрочным кредитам, которую регулятор поддерживает с помощью манипуляций на рынке государственных облигаций.
- Резервный Банк Новой Зеландии – Official Cash rate. Процентная ставка РБНЗ является инструментом для регулировки краткосрочных процентных ставок на финансовом рынке.
 Регулятор принимает от коммерческих банков средства на депозит с процентной ставкой на 0,25% меньше официальной и дает кредит со ставкой на 0,25% больше официальной.
Регулятор принимает от коммерческих банков средства на депозит с процентной ставкой на 0,25% меньше официальной и дает кредит со ставкой на 0,25% больше официальной. - Народный Банк Китая – Base interest rate. Процентная ставка Народного Банка Китая Base interest rate является ориентиром для базовых ставок коммерческих банков. Посредством изменения уровня ставки китайский регулятор оказывает влияние на все виды займов. Примечательно, что процентная ставка Народного Банка Китая из-за продолжительности финансового года всегда кратна 9.
Что такое процентная ставка LIBOR?
Процентная ставка LIBOR — это Лондонская межбанковская ставка предложения (англ. London Interbank Offered Rate или LIBOR) рассчитывается как средневзвешенная процентная ставка по межбанковским кредитам, предоставляемым банками, которые предлагают средства на сроки от 1 месяца до года в различных валютах.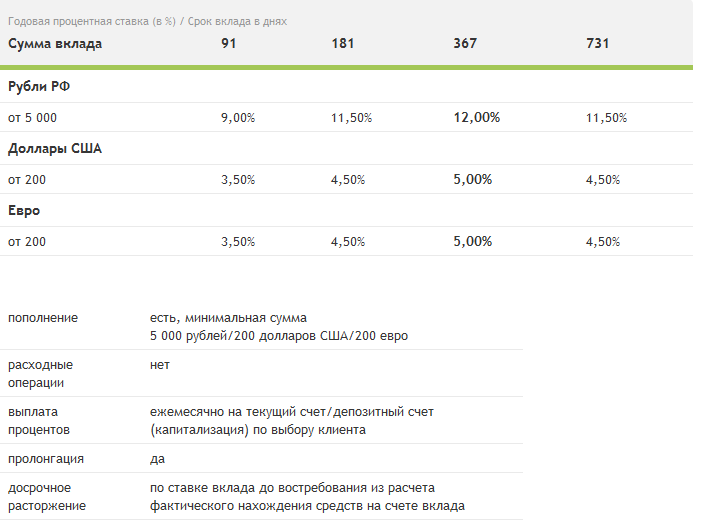
Она рассчитывается для таких валют как: доллар США, евро, японская иена, фунт стерлингов, датская и шведская крона, швейцарский франк, а также новозеландский, австралийский и канадский доллар.
Как определяется ставка LIBOR?
Ставку LIBOR фиксирует ассоциация банков Великобритании с 1985 года. Как уполномоченный агент банковской ассоциации Великобритании агентство Thomson Reuters ежедневно в 11:00 по западноевропейскому времени уточняет у 16 первоклассных банков цену предложения процентных ставок по стандартным срокам от 1 до 12 месяцев со спота. Далее по каждому периоду отбрасывают 4 самые высокие и 4 самые низкие ставки. Оставшиеся ставки составляют среднее арифметическое значение. Таким образом, образуется ставка LIBOR для каждого периода.
Зачем нужна LIBOR?
В глобальном масштабе ставка LIBOR – своего рода эталон процентной ставки по краткосрочным ссудам. Она необходима как ориентир для ставки рефинансирования целого ряда финансовых инструментов:
- фьючерсных контрактов по процентным ставкам на небольшие сроки;
- контрактов на размер процентной ставки в будущем.
 В таких соглашениях между двумя сторонами определяется величина ставки;
В таких соглашениях между двумя сторонами определяется величина ставки; - процентного свопа. Здесь стороны подписывают договор, подразумевающий обмен кредитными обязательствами на различных условиях, но при неизменной сумме. К примеру, «плавающая» ставка процента меняется на фиксированную при условии одновременного изменения типа валюты долга;
- синдицированного займа – передачи средств какому-то одному кредитополучателю от нескольких банков;
- облигаций с меняющейся процентной ставкой. Здесь речь идет о краткосрочном обязательстве, в котором время от времени производится пересмотр процентной ставки. Для расчета используется такой параметр, как доходность по государственным облигациям или межбанковским займам;
- различных валют, которые упоминались выше.
При расчете евро все чаще применяется другая процентная ставка – EURIBOR, которая принимается за основу на европейском межбанковском рынке.
В чем преимущество ставки LIBOR?
Процентная ставка LIBOR имеет ряд следующих преимуществ:
- Международное признание в качестве основного показателя для формирования ставки межбанковских кредитов.

- Возможность долгого периода использования.
- Доступный, понятный и простой механизм расчета параметров.
- Фиксинг по широкому спектру периодов кредитования и валют.
- Широкое применение в коммерческой сфере.
- Банки, данные которых применяются для расчетов, отличаются высоким кредитным рейтингом и повышенной надежностью.
- Возможность оперативного отслеживания текущей информации. По статистике около трети всех операций на рынке Форекс, а также пятой части межбанковских кредитных операций проходит именно в Лондоне. Основная доля всей товарно-сырьевых сделок в Еврозоне также проходит в столице Великобритании.
- Отсутствие требований к резервированию, что только способствует росту объемов рынка.
Полезные статьи по теме
Минимальная гарантированная процентная ставка по вкладу
Уважаемые клиенты!
АО «КУЗНЕЦКБИЗНЕСБАНК» в соответствии с Федеральным законом «О страховании вкладов физических лиц в банках Российской Федерации» № 177-ФЗ от 23. 12.2003 года (далее – «Закон»), информирует Вас о расчете минимальной гарантированной процентной ставки по вкладу (счету) (далее – минимальная гарантированная ставка)
12.2003 года (далее – «Закон»), информирует Вас о расчете минимальной гарантированной процентной ставки по вкладу (счету) (далее – минимальная гарантированная ставка)
Минимальную гарантированную ставку рекомендуется рассчитывать в процентах годовых по формуле (далее – формула расчета ставки):
где:
Минимальная гарантированная ставка – гарантированная ставка, выраженная в процентах годовых. Дробное значение минимальной гарантированной ставки округляется до трех десятичных знаков после запятой по математическим правилам округления;
P — сумма процентов, которые кредитная организация обязана начислить и уплатить вкладчику на минимальную сумму вклада (денежных средств),
соответствующую значению показателя «D» формулы расчета ставки, в порядке и в размере, установленном соответствующим договором, при условии хранения вклада до истечения его срока, и без учета условий, предусматривающих возможность увеличения процентного дохода по договору, в том числе в случаях заключения (расторжения) вкладчиком иного договора и/или получения им дополнительной услуги, не связанных с размещением денежных средств во вклад (зачислением денежных средств на счет). Если начисление процентов осуществляется с использованием плавающей ставки (процентной ставки, содержащей переменные величины), при расчете минимальной гарантированной ставки применяется значение переменной величины по состоянию на дату заключения договора;
Если начисление процентов осуществляется с использованием плавающей ставки (процентной ставки, содержащей переменные величины), при расчете минимальной гарантированной ставки применяется значение переменной величины по состоянию на дату заключения договора;
D – минимальная сумма вклада (денежных средств). Указывается минимальная сумма вклада (денежных средств), достаточная в соответствии с условиями соответствующего договора банковского вклада для его открытия.
В случае отсутствия в договоре банковского вклада вышеуказанного условия, показатель «D» принимается в значении, равном 1 рублю. По договорам банковского вклада, предусматривающим внесение вкладов в иностранной валюте, показатель «D» принимается равным минимальной сумме вклада в соответствующей валюте вклада;
d — количество календарных дней, на которое в соответствии с договором привлечен вклад (срок вклада).
По договорам банковского вклада до востребования, а также договорам банковского счета минимальную гарантированную ставку рекомендуется рассчитывать исходя из предположения, что соответствующий договор будет прекращен через действительное число календарных дней в году (365 или 366 дней соответственно).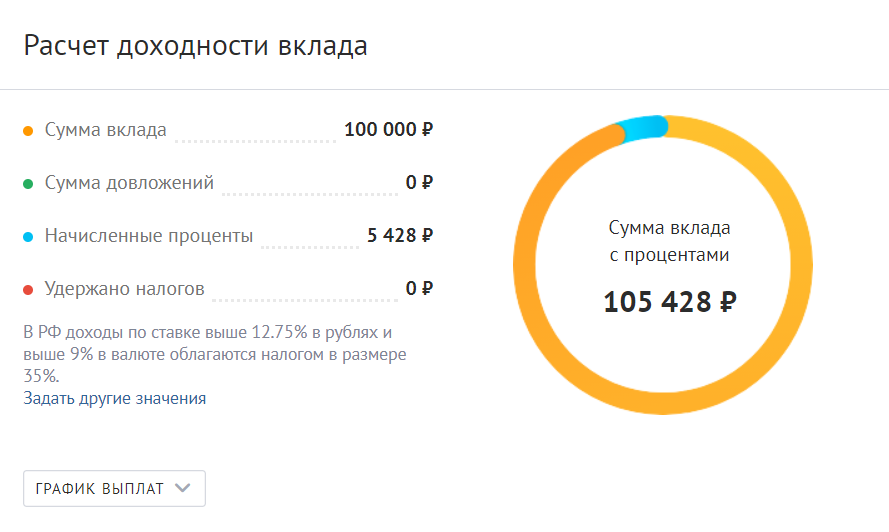 В случае если в договоре банковского вклада до востребования или в договоре банковского счета содержится условие о том, что в зависимости от срока нахождения денежных средств во вкладе до востребования (на счете) процентный доход по договору изменяется, при расчете минимальной гарантированной ставки показатель «d» принимается равным сроку, при котором процентный доход будет минимальным.
В случае если в договоре банковского вклада до востребования или в договоре банковского счета содержится условие о том, что в зависимости от срока нахождения денежных средств во вкладе до востребования (на счете) процентный доход по договору изменяется, при расчете минимальной гарантированной ставки показатель «d» принимается равным сроку, при котором процентный доход будет минимальным.
654080, Кемеровская обл., г.Новокузнецк, ул. Кирова 89б, тел. приемной (3843)76-32-40, факс (3843)76-60-90, e-mail: [email protected], kbb.ru 30101810600000000740 в РКЦ Новокузнецк БИК 043209740 ИНН/КПП 4216004076 / 421701001, ОГРН 1024200001814, ОКПО 09800185
Эффективная годовая ставка (EAR) — Как рассчитать эффективную процентную ставку
Что такое эффективная годовая процентная ставка?
Эффективная годовая процентная ставка (EAR) — это процентная ставка, скорректированная с учетом начисления сложных темпов роста Совокупный темп роста — это мера, используемая специально в контексте бизнеса и инвестирования, которая указывает темпы роста за несколько периодов времени. Это показатель постоянного роста ряда данных. Самым большим преимуществом совокупной скорости роста является то, что метрика учитывает эффект сложения.за определенный период. Проще говоря, эффективная годовая процентная ставка — это процентная ставка. Процентные расходы. Процентные расходы возникают из-за компании, которая финансирует за счет заемных средств или аренды капитала. Процентная ставка указывается в отчете о прибылях и убытках, но также может указываться, что инвестор может заработать (или заплатить) через год после учета сложного процента.
Это показатель постоянного роста ряда данных. Самым большим преимуществом совокупной скорости роста является то, что метрика учитывает эффект сложения.за определенный период. Проще говоря, эффективная годовая процентная ставка — это процентная ставка. Процентные расходы. Процентные расходы возникают из-за компании, которая финансирует за счет заемных средств или аренды капитала. Процентная ставка указывается в отчете о прибылях и убытках, но также может указываться, что инвестор может заработать (или заплатить) через год после учета сложного процента.
EAR можно использовать для оценки процентов, подлежащих уплате по ссуде или долгу, или для оценки доходов от инвестиций, таких как гарантированный инвестиционный сертификат (GIC) или сберегательный счет.
Эффективная годовая процентная ставка также известна как эффективная процентная ставка (EIR), годовая эквивалентная ставка (AER) или эффективная ставка. Сравните это с годовой процентной ставкой (APR). Годовая процентная ставка (APR) Годовая процентная ставка (APR) — это годовая процентная ставка, которую физическое лицо должно платить по ссуде или которую они получают на депозитный счет. В конечном итоге, годовая процентная ставка — это простой процентный термин, используемый для выражения числовой суммы, ежегодно выплачиваемой физическим или юридическим лицом за право заимствования денег.который основан на простом интересеПростой интересПростой процентной формуле, определении и примере. Простой процент — это расчет процентов, который не учитывает эффект начисления сложных процентов. Во многих случаях проценты складываются с каждым назначенным периодом ссуды, но в случае простых процентов это не так. Расчет простых процентов равен основной сумме, умноженной на процентную ставку, умноженной на количество периодов.
Годовая процентная ставка (APR) Годовая процентная ставка (APR) — это годовая процентная ставка, которую физическое лицо должно платить по ссуде или которую они получают на депозитный счет. В конечном итоге, годовая процентная ставка — это простой процентный термин, используемый для выражения числовой суммы, ежегодно выплачиваемой физическим или юридическим лицом за право заимствования денег.который основан на простом интересеПростой интересПростой процентной формуле, определении и примере. Простой процент — это расчет процентов, который не учитывает эффект начисления сложных процентов. Во многих случаях проценты складываются с каждым назначенным периодом ссуды, но в случае простых процентов это не так. Расчет простых процентов равен основной сумме, умноженной на процентную ставку, умноженной на количество периодов.
Формула EAR приведена ниже:
Где:
- i = Заявленный годовой процент ставка
- n = Количество периодов начисления сложных процентов
Эффективная годовая ставка на основе начисления процентов
В таблице ниже показана разница в эффективной годовой ставке при изменении периодов начисления сложных процентов.
Таблица: Курс CFI по основам фиксированного дохода
Например, EAR заявленной процентной ставки 1%, начисляемой ежеквартально, составляет 1,0038%.
Важность эффективной годовой ставки
Эффективная годовая процентная ставка — важный инструмент, позволяющий оценить истинную доходность инвестиций или истинную процентную ставку по ссуде.
Заявленная годовая процентная ставка и эффективная процентная ставка могут значительно отличаться из-за начисления сложных процентов.Эффективная процентная ставка важна для определения наилучшего кредита или определения того, какие инвестиции предлагают самую высокую норму доходности. Внутренняя норма доходности (IRR) Внутренняя норма доходности (IRR) — это ставка дисконтирования, которая составляет чистую приведенную стоимость (NPV). ) нулевого проекта. Другими словами, это ожидаемая совокупная годовая норма прибыли, которая будет получена от проекта или инвестиций.
В случае начисления сложных процентов EAR всегда выше установленной годовой процентной ставки.
EAR Пример
Например, предположим, что банк предлагает вашему депозиту в размере 10 000 долларов США установленную процентную ставку 12%, начисляемую ежемесячно.В приведенной ниже таблице демонстрируется концепция эффективной годовой процентной ставки:
Таблица: Курс CFI по основам фиксированного дохода
Процентная ставка за 1 месяц: начальный баланс (10 000 долларов США) x процентная ставка (12% / 12 = 1%). ) = 100 долларов США
Процентная ставка за месяц 2: Начальный баланс (10 100 долларов США) x процентная ставка (12% / 12 = 1%) = 101 доллар США
Изменение в процентах от начального баланса (10000 долларов США) до конечного баланса ( 11 268 долларов США) равно (11 268 долларов США — 10 000 долларов США) / 10 000 долларов США =.12683 или 12,683%, что является эффективной годовой процентной ставкой. Несмотря на то, что банк предложил заявленную процентную ставку 12%, ваши деньги выросли на 12,683% за счет ежемесячного начисления сложных процентов.
Эффективная годовая процентная ставка позволяет определить истинную рентабельность инвестиций (ROI) Формула ROI (Return on Investment) Рентабельность инвестиций (ROI) — это финансовый коэффициент, используемый для расчета выгоды, которую инвестор получит по отношению к своим инвестициям. Стоимость. Чаще всего он измеряется как чистая прибыль, деленная на первоначальные капитальные затраты на инвестиции.Чем выше коэффициент, тем больше полученная выгода.
Скачать бесплатный шаблон
Введите свое имя и адрес электронной почты в форму ниже и загрузите бесплатный шаблон, показанный выше!
Калькулятор эффективной годовой процентной ставки
Загрузите бесплатный шаблон Excel, чтобы углубить свои знания в области финансов!
Как рассчитать эффективную процентную ставку?
Чтобы рассчитать эффективную процентную ставку по формуле EAR, выполните следующие действия:
1.Определите заявленную процентную ставку
Заявленную процентную ставку (также называемую годовой процентной ставкой или номинальной ставкой) обычно можно найти в заголовках кредитного или депозитного договора. Пример: «Годовая ставка 36%, проценты взимаются ежемесячно».
Пример: «Годовая ставка 36%, проценты взимаются ежемесячно».
2. Определите количество периодов начисления сложных процентов
Периоды начисления сложных процентов обычно бывают ежемесячными или ежеквартальными. Периоды начисления сложных процентов могут составлять 12 (12 месяцев в году) и 4 квартальных (4 квартала в году).
Для справки:
- Ежемесячно = 12 периодов начисления начислений
- Квартально = 4 периода начисления начислений
- Двухнедельные = 26 периодов начисления начислений
- Еженедельно = 52 периода начисления начислений
- Ежедневно = 365 периодов начисления начислений
3 .Примените формулу EAR: EAR = (1+ i / n)
n — 1
Где:
- i = заявленная процентная ставка
- n = периоды начисления процентов
Пример
Для расчета эффективной годовой процентной ставки по кредитной карте с годовой ставкой 36% и ежемесячным начислением процентов:
1. Заявленная процентная ставка: 36%
Заявленная процентная ставка: 36%
2. Количество периодов начисления сложных процентов: 12
Таким образом, EAR = (1 + 0.12 — 1 = 0,4257 или 42,57%.
Почему банки не используют эффективную годовую процентную ставку?
Когда банки взимают проценты, вместо эффективной годовой процентной ставки используется указанная процентная ставка. Это делается для того, чтобы потребители поверили, что они платят более низкую процентную ставку.
Например, для ссуды с установленной процентной ставкой 30%, начисляемой ежемесячно, эффективная годовая процентная ставка будет 34,48%. Банки обычно рекламируют заявленную процентную ставку 30%, а не эффективную процентную ставку 34.48%.
Когда банки выплачивают проценты по вашему депозитному счету, EAR объявляется более привлекательным, чем заявленная процентная ставка.
Например, для депозита с установленной ставкой 10% ежемесячно, эффективная годовая процентная ставка будет 10,47%. Банки будут рекламировать эффективную годовую процентную ставку 10,47%, а не заявленную процентную ставку в 10%.
По сути, они показывают ту ставку, которая кажется более благоприятной.
Дополнительная литература
CFI — глобальный провайдер курсов финансового моделирования и сертификации финансового аналитика Стань сертифицированным аналитиком финансового моделирования и оценки (FMVA) ® Сертификация CFI по финансовому моделированию и оценке (FMVA) ® поможет вам обрести уверенность в себе. необходимость в вашей финансовой карьере.Запишитесь сегодня !. Чтобы продолжить карьеру финансового профессионала, ознакомьтесь со следующими дополнительными ресурсами CFI:
- Ожидаемая доходность Ожидаемая доходность Ожидаемая доходность инвестиций — это ожидаемая величина распределения вероятностей возможной прибыли, которую они могут предоставить инвесторам. Доходность инвестиций — это неизвестная переменная, у которой разные значения, связанные с разными вероятностями.
- Базовые точки Базисные точки (BPS) Базовые точки (BPS) — это обычно используемая метрика для измерения изменений процентных ставок.
 Базисная точка — одна сотая процента.
Базисная точка — одна сотая процента. - Прирост капитала YieldCapital Прирост Доходность Доходность прироста капитала (CGY) — это увеличение цены инвестиции или ценной бумаги, выраженное в процентах. Поскольку расчет доходности от прироста капитала включает рыночную цену ценной бумаги с течением времени, его можно использовать для анализа колебаний рыночной цены ценной бумаги. См. Расчет и пример
- Средневзвешенная стоимость капитала (WACC) WACCWACC — это средневзвешенная стоимость капитала компании, которая представляет собой смешанную стоимость капитала, включая собственный капитал и заемные средства.
Определение эффективной годовой процентной ставки
Что такое эффективная годовая процентная ставка?
Эффективная годовая процентная ставка — это реальная доходность сберегательного счета или любых инвестиций с выплатой процентов, если принять во внимание эффекты начисления сложных процентов с течением времени. Он также показывает реальную процентную ставку по процентам по ссуде, кредитной карте или любой другой задолженности.
Ее также называют эффективной процентной ставкой, эффективной ставкой или годовой эквивалентной ставкой.n-1 \\ & \ textbf {где:} \\ & i = \ text {Номинальная процентная ставка} \\ & n = \ text {Количество периодов} \\ \ end {выровнено}
Эффективная годовая процентная ставка = (1 + ni) n − 1, где: i = номинальная процентная ставка = количество периодов
Эффективная годовая процентная ставка
О чем говорит эффективная годовая процентная ставка?
Банковский депозитный сертификат, сберегательный счет или предложение ссуды могут рекламироваться с указанием номинальной процентной ставки, а также эффективной годовой процентной ставки.Номинальная процентная ставка не отражает эффекты начисления сложных процентов или даже комиссий, связанных с этими финансовыми продуктами. Эффективная годовая процентная ставка — это реальный доход.
Ключевые выводы
- Сберегательный счет или ссуда могут рекламироваться как с номинальной процентной ставкой, так и с эффективной годовой процентной ставкой.

- Эффективная годовая процентная ставка — это реальный доход, выплачиваемый на сбережения, или реальная стоимость ссуды, поскольку она учитывает эффекты начисления сложных процентов и любые взимаемые комиссии.
- Чем чаще периоды начисления сложных процентов, тем выше доход.
Вот почему эффективная годовая процентная ставка — важная финансовая концепция, которую необходимо понять. Точно сравнивать различные предложения можно только в том случае, если вы знаете эффективные годовые процентные ставки по каждому из них.
Пример эффективной годовой процентной ставки
Например, рассмотрим эти два предложения: Инвестиция A платит 10% годовых, начисляемых ежемесячно. Инвестиции B выплачиваются 10,1% каждые полгода.Какое предложение лучше?
В обоих случаях рекламируемая процентная ставка является номинальной процентной ставкой. Эффективная годовая процентная ставка рассчитывается путем корректировки номинальной процентной ставки в зависимости от количества периодов начисления сложных процентов, которые будут иметь место для финансового продукта за период времени. (количество периодов начисления сложных процентов) — 1
(количество периодов начисления сложных процентов) — 1
Инвестиция B имеет более высокую заявленную номинальную процентную ставку, но эффективная годовая процентная ставка ниже, чем эффективная ставка для инвестиции A. Это связано с тем, что инвестиции B составляют меньше раз в течение года.
Если инвестор вложит, скажем, 5 000 000 долларов в одну из этих инвестиций, неправильное решение будет стоить более 5 800 долларов в год.
Более частое начисление сложных процентов дает более высокую прибыль
По мере увеличения количества периодов начисления сложных процентов увеличивается и эффективная годовая процентная ставка.Квартальное начисление сложных процентов дает более высокую доходность, чем полугодовое начисление сложных процентов, ежемесячное начисление сложных процентов больше, чем ежеквартально, а ежедневное начисление сложных процентов больше, чем ежемесячно. Ниже приводится разбивка результатов этих различных составных периодов с номинальной процентной ставкой 10%:
- Полугодовые = 10,250%
- Ежеквартально = 10,381%
- Ежемесячно = 10,471%
- Ежедневно = 10,516%
Пределы компаундирования
Есть потолок феномену компаундирования.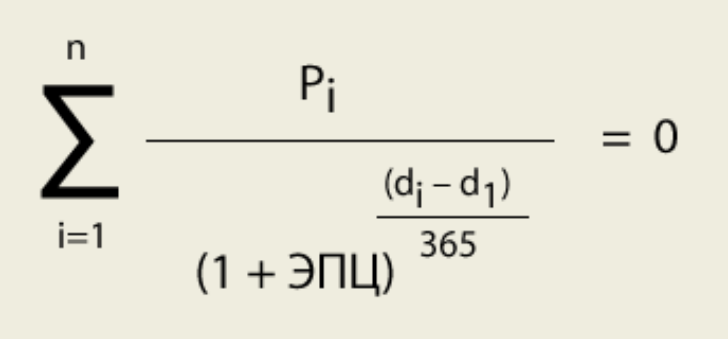 (0,1) — 1.
(0,1) — 1.
Часто задаваемые вопросы
Какова эффективная годовая процентная ставка?
Эффективная годовая процентная ставка — это важное понятие, описывающее истинную процентную ставку, связанную с инвестициями или ссудой. Наиболее важной особенностью эффективной годовой процентной ставки является то, что она учитывает тот факт, что более частые периоды начисления сложных процентов приведут к более высокой эффективной процентной ставке. Например, предположим, что у вас есть две ссуды, каждая из которых имеет установленную процентную ставку 10%, в которой один составляет ежегодно, а другой — два раза в год.Несмотря на то, что у них обоих заявленная процентная ставка составляет 10%, эффективная годовая процентная ставка по ссуде, составляющей два раза в год, будет выше.
Как рассчитать эффективную годовую процентную ставку?
Эффективная годовая процентная ставка рассчитывается по следующей формуле:
Взаимодействие с другими людьми
E
ж
ж
е
c
т
я
v
е
А
п
п
ты
а
л
я
п
т
е
р
е
s
т
р
а
т
е
знак равно
(
1
+
я
п
)
п
—
1
куда:
я
знак равно
Номинальная процентная ставка
п
знак равно
Количество периодов
\ begin {align} & Effective \ Annual \ Interest \ Rate = \ left (1+ \ frac {i} {n} \ right) ^ n-1 \\ & \ textbf {где:} \\ & i = \ text {Номинальный процентная ставка} \\ & n = \ text {Количество периодов} \\ \ end {выровнено}
Эффективная годовая процентная ставка = (1 + ni) n − 1, где: i = номинальная процентная ставка = количество периодов
Хотя это можно сделать вручную, большинство инвесторов будут использовать финансовый калькулятор, электронную таблицу или онлайн-программу.Более того, инвестиционные веб-сайты и другие финансовые ресурсы регулярно публикуют эффективную годовую процентную ставку ссуды или инвестиции. Эта цифра также часто включается в проспект эмиссии и маркетинговые документы, подготовленные эмитентами ценных бумаг.
Почему важна эффективная годовая процентная ставка?
Эффективная годовая процентная ставка важна, потому что без нее заемщики могут быть введены в заблуждение и недооценивают истинную стоимость ссуды. Это, в свою очередь, может привести к финансовым проблемам, если заемщик не внесет в бюджет полную сумму своих процентных платежей.Для инвесторов, с другой стороны, расчет эффективной годовой процентной ставки важен для прогнозирования фактического ожидаемого дохода от инвестиций, таких как корпоративные облигации или другие ценные бумаги с фиксированным доходом. В противном случае они могут недооценить реальную привлекательность инвестиционной возможности.
Разъяснение процентных ставок
: номинальная, реальная, эффективная
Какие разные процентные ставки?
Термин «процентная ставка» — одна из наиболее часто используемых фраз в лексике инвестиций с фиксированным доходом.Различные типы процентных ставок, включая реальные, номинальные, эффективные и годовые, отличаются ключевыми экономическими факторами, которые могут помочь людям стать более умными потребителями и более проницательными инвесторами.
Ключевые выводы
- Различные типы процентных ставок, такие как реальная, номинальная, эффективная и годовая, отличаются критическими экономическими факторами.
- Номинальная процентная ставка или купонная ставка — это фактическая цена, которую заемщики платят кредиторам, без учета каких-либо других экономических факторов.
- Реальная процентная ставка учитывает инфляцию, давая более точное представление о покупательной способности заемщика после погашения позиции.
- Эффективная процентная ставка включает влияние начисления процентов, при котором по облигации проценты могут выплачиваться ежегодно, но составлять проценты раз в полгода, увеличивая общую доходность.
Номинальная процентная ставка
Номинальная процентная ставка — это заявленная процентная ставка по облигации или ссуде, которая означает фактическую денежную цену, которую заемщики платят кредиторам за использование своих денег.Если номинальная ставка по ссуде составляет 5%, заемщики могут рассчитывать на выплату 5 долларов процентов за каждые 100 долларов, предоставленных им в ссуду. Это часто называют купонной ставкой, потому что она традиционно указывается на купонах, выкупаемых держателями облигаций.
Реальная процентная ставка
Реальная процентная ставка названа так потому, что, в отличие от номинальной, она учитывает инфляцию в уравнении, чтобы дать инвесторам более точную оценку своей покупательной способности после того, как они выкупят свои позиции. Если по облигации с ежегодным начислением сложных процентов номинальная доходность составляет 6%, а уровень инфляции составляет 4%, то реальная процентная ставка на самом деле составляет всего 2%.
Особые соображения
Реальные процентные ставки могут оказаться в отрицательной зоне, если уровень инфляции превышает номинальную ставку инвестиций. Например, облигация с номинальной ставкой 3% будет иметь реальную процентную ставку -1%, если уровень инфляции составляет 4%. Сравнение реальных и номинальных процентных ставок можно рассчитать с помощью этого уравнения:
Взаимодействие с другими людьми
RR
знак равно
Номинальная процентная ставка
—
Уровень инфляции
куда:
RR = Реальная норма прибыли
\ begin {align} & \ text {RR} = \ text {Номинальная процентная ставка} — \ text {Inflation Rate} \\ & \ textbf {где:} \\ & \ text {RR = Real Rate Return} \\ \ end {выровнен}
RR = номинальная процентная ставка — уровень инфляции, где: RR = реальная ставка дохода.
Из этой формулы можно вывести несколько экономических условий, которые кредиторы, заемщики и инвесторы могут использовать для выработки более обоснованных финансовых решений.
- Обычно, когда уровень инфляции отрицательный (дефляционный), реальные ставки превышают номинальные. Но верно обратное, когда темпы инфляции положительные.
- Согласно одной из теорий, уровень инфляции со временем изменяется вместе с номинальными процентными ставками, а это означает, что реальные процентные ставки становятся стабильными в течение длительных периодов времени. Следовательно, инвесторы с более длительными временными горизонтами могут более точно оценить доходность своих инвестиций с поправкой на инфляцию.
Эффективная процентная ставка
Инвесторы и заемщики также должны знать эффективную процентную ставку, которая учитывает концепцию начисления сложных процентов. Например, если по облигации выплачивается 6% годовых и складывается раз в полгода, инвестор, разместивший 1000 долларов США в эту облигацию, получит 30 долларов процентных платежей по истечении первых 6 месяцев (1000 долларов x 0,03) и 30,90 долларов США процентов по прошествии следующих шести месяцев ( 1030 долларов США x 0,03). В сумме этот инвестор получает 60,90 долларов за год.В этом сценарии, хотя номинальная ставка составляет 6%, эффективная ставка составляет 6,09%.
С математической точки зрения, разница между номинальной и эффективной ставками увеличивается с увеличением количества периодов начисления сложных процентов в течение определенного периода времени.
Силы за процентными ставками
Приложения
Когда речь идет о займах, важна разница между номинальной, реальной и эффективной ставками. Например, ссуда с частыми периодами начисления сложных процентов будет дороже, чем ссуда с ежегодным начислением, что является жизненно важным соображением при покупке ипотечных кредитов.
Более того, облигация, по которой реальная процентная ставка составляет всего 1%, может не обеспечить адекватного роста активов инвестора с течением времени. Проще говоря: процентные ставки эффективно показывают истинную прибыль от инвестиций с фиксированным доходом и истинную стоимость заимствования для физических или юридических лиц.
СОВЕТЫ и другие альтернативы
Инвесторы, которые ищут защиты от инфляции в сфере фиксированного дохода, могут решить рассмотреть казначейские ценные бумаги с защитой от инфляции (TIPS), по которым выплачиваются процентные ставки, индексированные с учетом инфляции.Паевые инвестиционные фонды, инвестирующие в облигации, ипотечные кредиты и приоритетные обеспеченные ссуды с плавающей процентной ставкой, также периодически корректируются в соответствии с текущими ставками.
Итог
Когда дело доходит до процентных ставок по облигациям, проницательные инвесторы знают, что при рассмотрении своих общих инвестиционных целей не следует ограничиваться номинальными или купонными ставками. Квалифицированный финансовый консультант может помочь инвесторам сориентироваться в процентных ставках, которые соответствуют инфляции.
Какова эффективная годовая процентная ставка? — Определение | Значение
Определение: Эффективная годовая процентная ставка или годовая эквивалентная ставка, полученная или выплаченная, — это фактическая ставка, полученная с учетом периодов начисления сложных процентов.
Что означает эффективная процентная ставка?
Что такое эффективная процентная ставка? На основе заявленной или номинальной ставки за определенный период, например годовой процентной ставки, эффективная ставка рассчитывается путем включения влияния периодов начисления сложных процентов в заявленную номинальную ставку. Формула эффективной процентной ставки рассчитывается так:
Целью расчета эффективной ставки по любому финансовому инструменту является получение точного представления об истинных процентах, полученных или выплаченных за определенный период времени.Хотя финансовое учреждение может предложить что-то вроде ипотечной ссуды с годовой процентной ставкой 4,5%, важно понимать, что количество периодов, в течение которых выплачиваются проценты в течение годового срока, будет влиять на истинную эффективную ставку ссуды.
Давайте рассмотрим простой пример.
Пример
Давайте представим, что это ваш счастливый день, и вы выиграли единовременный приз в местном розыгрыше. После получения единовременной выплаты и уплаты необходимых налогов и сборов вы получаете 10 000 долларов! Теперь, предполагая, что вы не зависите от денег, вы решаете вложить деньги в безопасное вложение, например, в депозитный сертификат в местном банке.Два банка в вашем районе имеют привлекательные предложения, банк A предлагает 5-летний депозитный сертификат с годовой процентной ставкой 4%, с начислением процентов, а банк B предлагает 5-летний депозитный сертификат с годовой процентной ставкой 4%, с начислением сложных процентов. ежемесячно.
Проще говоря, правила начисления сложных процентов гласят, что чем больше процентных ставок увеличивается за определенный период, тем лучше эффективная ставка, но для целей нашего примера мы хотим понять истинную эффективную ставку каждого варианта и ее размер. сделает нас!
Используя приведенное выше уравнение, банк A может предложить эффективную процентную ставку 5.095% в год, рассчитывается по следующей формуле:
Банк B будет предлагать эффективную процентную ставку 5,116% в год, рассчитанную по следующему уравнению:
В результате быстрого расчета, в ваших интересах внести свой выигрыш в предложение о депозитном сертификате банка B!
Краткое определение
Определите эффективную процентную ставку: Эффективная годовая ставка означает фактическую процентную ставку по инструменту, рассчитанную с использованием сложных процентов.
Номинальные, периодические и эффективные процентные ставки
Номинальные, периодические и эффективные процентные ставки, основанные на дискретном начислении процентов
Обычно финансовые агентства сообщают процентную ставку на номинальной годовой основе с указанным периодом начисления сложных процентов, который показывает, сколько раз начисляются проценты в год. Это называется простой процентной ставкой, номинальной процентной ставкой или годовой процентной ставкой. Если процентная ставка начисляется ежегодно, это означает, что проценты начисляются один раз в год, и вы получаете проценты в конце года.Например, если вы поместите 100 долларов на банковский счет с годовой процентной ставкой 6% годовых, вы получите 100 * (1 + 0,06) = 106 долларов в конце года.
Но период начисления сложных процентов может быть меньше года (он может быть квартальным, ежемесячным или ежедневным). В этом случае процентная ставка будет увеличиваться более одного раза в год. Например, если финансовое агентство отчитывается о квартальном начислении сложных процентов, это означает, что проценты будут начисляться четыре раза в год, и вы будете получать проценты в конце каждого квартала.Если проценты начисляются ежемесячно, тогда проценты начисляются 12 раз в год, и вы получите проценты в конце месяца.
Например: предположим, что вы кладете 100 долларов на банковский счет, и банк ежемесячно выплачивает вам 6% годовых. Это означает, что номинальная годовая процентная ставка составляет 6%, проценты начисляются каждый месяц (12 раз в год) по ставке 6/12 = 0,005 в месяц, и вы получаете проценты в конце каждого месяца. В этом случае в конце года вы получите 100 * (1 + 0.005) 12 = 106,17 долларов, что больше, чем при начислении раз в год: 100 * (1 + 0,06) 1 = 106 долларов. Следовательно, чем больше периодов начисления сложных процентов в году, тем больше общая сумма выплачиваемых процентов.
Пожалуйста, посмотрите следующее видео, Номинальная и периодическая процентная ставка (время 3:52).
Номинальные и периодические процентные ставки
Щелкните, чтобы увидеть стенограмму видео «Номинальные и периодические процентные ставки».
ВЕДУЩИЙ
: В этом видео я собираюсь объяснить номинальные, периодические и эффективные процентные ставки.Финансовые агентства обычно сообщают процентную ставку ежегодно. Процентная ставка может увеличиваться один или несколько раз в год. Если процентная ставка начисляется ежегодно, это означает, что процентная ставка начисляется один раз в год. Если процентная ставка начисляется ежеквартально, то процентная ставка увеличивается четыре раза в год. И если процентная ставка начисляется ежемесячно, это означает, что процентная ставка увеличивается 12 раз в год.
Давайте поработаем на примере. Предположим, вы вкладываете 100 долларов на воображаемый банковский счет, который дает вам 6% годовых, начисляемых ежегодно.Таким образом, номинальная процентная ставка составляет 6% годовых. Процентная ставка в размере 6% начисляется один раз в год, и вы получите проценты и основную сумму своих денег в конце первого года. Таким образом, вы получите 100 долларов, умноженные на 1, плюс 6% в степени 1 в конце первого года, что равняется 106 долларам.
Теперь предположим, что банк выплачивает вам 6% годовых, начисляемых ежеквартально. Таким образом, это означает, что номинальная процентная ставка составляет 6% в квартал, или процентная ставка будет увеличиваться четыре раза в год, а процентная ставка рассчитывается в конце каждого квартала.Чтобы рассчитать сумму денег, которую вы получите в конце первого года, нам необходимо рассчитать процентную ставку за период, которая будет составлять 6%, разделенные на 4, и это равняется 1,5%. Вы вносите свои 100 долларов в настоящее время, и банк начисляет проценты по ставке 1,5% за квартал. В году четыре квартала, поэтому проценты будут начисляться четыре раза в год по ставке 1,5% за квартал. Затем, в конце года, вы получите 100 долларов, умноженные на 1 плюс 0,15 в степени 4, что равняется 106 долларам плюс 0 долларов.14. Как видите, если банк учитывает процентную ставку, которая начисляется ежеквартально, он даст вам немного более высокий процент по сравнению со случаем, когда процентная ставка начисляется ежегодно.
Теперь предположим, что банк выплачивает вам 6% начисленных процентов ежемесячно, что означает, что процентная ставка начисляется 12 раз в год. В этом случае банк начисляет проценты каждый месяц. И, как и в предыдущем примере, процентная ставка за период будет 6%, деленная на 12, что составит 0,5% в месяц.И вы получите 100 долларов, умноженные на 1, плюс 0,005 в степени 12, что равняется 106 долларам плюс 0,17 доллара. Потому что существует 12 периодов начисления сложных процентов, а процентная ставка за период составляет 0,5%. Как видите, процентная ставка начисляется ежемесячно, поэтому в конце года вы получите немного больше денег. Чем больше у вас начислений сложных процентов в год, тем выше будут проценты в конце года.
Кредит: Фарид Тайари
Процентная ставка за период i = r / m
Где m = количество периодов начисления сложных процентов в год
r = номинальная процентная ставка = mi
« Эффективная процентная ставка — это процентная ставка, которая при применении один раз в год к основной сумме дает такую же сумму процентов, равную номинальной ставке r процентов в год, начисляемой m раз в год.Годовая процентная доходность (APY) — это стандартный термин, используемый в банковской сфере для определения эффективной процентной ставки. «
Будущая стоимость, F1 , инвестирования P при и % за период на м за период после одного года:
| п. | _ | _ | _ | _ | _ | F1 = P (F / P i, m ) = P (1 + i) m |
| 0 | 1 | 2 | … | м периодов в год | ||
И если эффективная процентная ставка E, применяется один раз в год, то будущая стоимость, F2 , инвестирования P по цене E% в год:
| п. | _ | _ | F2 = P (F / P E, 1 ) = P (1 + E) 1 | |||
| 0 | 1 период в год | |||||
Тогда:
F1 = F2P (1 + i) m = P (1 + E) 1
Начиная с P одинаково с обеих сторон: (1 + i) m = E + 1
Тогда:
Эффективная годовая процентная ставка: E = (1 + i) m − 1
(Уравнение 2-1)
Если эффективная годовая процентная ставка E известна, а процентная ставка за эквивалентный период i неизвестна, уравнение 2-1 может быть записано как:
я = (E +1) 1 / м −1
(Уравнение 2-2)
Возвращаясь к предыдущему примеру, i = 6/12 = 0.005so, E = (1 + 0,005) 12−1 = 1,0617 — 1 = 0,0617 или 6,17%
Посмотрите следующее видео , Эффективная процентная ставка (время 4:02).
Эффективная процентная ставка
Щелкните, чтобы увидеть стенограмму видео «Эффективная процентная ставка».
ВЕДУЩИЙ
: В этом видео я собираюсь объяснить, как рассчитать эффективную процентную ставку. В предыдущем видео мы узнали, как рассчитать процентную ставку за период, которая представляет собой номинальную процентную ставку r, деленную на количество периодов начисления сложных процентов в году, m.Таким образом, чтобы рассчитать будущую стоимость, вам нужно знать количество периодов от настоящего времени и желаемого будущего, а также процентную ставку за период. Например, f, будущее значение на конец первого года равно p, умножьте 1 на i, степень m, где m — количество периодов начисления сложных процентов в год.
Эффективная процентная ставка — это процентная ставка, которая при применении один раз в год дает вам такую же сумму процентов, равную номинальной ставке r. Годовая процентная доходность или APY — это термин, который используется в банковской сфере для обозначения эффективной процентной ставки.Вы можете увидеть здесь, когда где-то читаете, что, например, процентная ставка составляет 6% ежемесячно, это немного сбивает с толку. Потому что он не сообщает вам, какой будет фактическая годовая процентная ставка. Эффективная процентная ставка — это ставка, которая нам здесь помогает. Эффективная процентная ставка — это годовая ставка, которая дает вам точно такой же процент, равный номинальной ставке, которая начисляется несколько раз в год.
Возвращаясь к примеру в предыдущем видео, вы видели, что если вы поместите 100 долларов на банковский счет, который дает вам 6% -ную ежемесячную процентную ставку, вы получите 106 долларов плюс 0 долларов.17 в год. Таким образом, вы можете предположить, что эффективная процентная ставка здесь может составлять 6,17%. Теперь посмотрим, сможем ли мы найти общее уравнение. На предыдущем слайде я объяснил, как мы рассчитываем будущее значение F1 в конце первого года на основе процентной ставки периода i и количества периодов начисления сложных процентов в году m.
Если вы хотите рассчитать будущую стоимость в конце первого года, используя эффективную процентную ставку, здесь мы показываем это, у нас будет F2, равное P, умножить 1 плюс E в степени 1. Эффективная процентная ставка — E И мы хотим, чтобы рассчитать будущую стоимость в конце первого года.Будущая стоимость денег в конце первого года с использованием процентной ставки за период и эффективной процентной ставки должна быть равна. Значит, F1 должен быть равен F2.
И у нас есть уравнение 2-1. Это уравнение можно записать для i. E — эффективная процентная ставка. m — количество периодов начисления сложных процентов в году, а i — процентная ставка за период. Возвращаясь к примеру из предыдущего видео, мы положили 800 долларов на банковский счет, который дает нам 6% начисленных процентов ежемесячно. Чтобы вычислить эффективную процентную ставку, нам нужно сначала вычислить процентную ставку за период, а затем использовать только что извлеченное уравнение.Таким образом, эффективная процентная ставка будет 6,17%, что означает, что если мы применим процентную ставку 6,17% в год, это даст нам точно такую же будущую ценность, как и применение процентной ставки в размере 6%, начисленной ежемесячно.
Кредит: Фарид Тайари
Пример 2-1:
Предположим, что инвестиция приносит вам 2000 долларов в конце первого, второго и третьего года с годовой процентной ставкой 12%, начисляемой ежеквартально. Рассчитайте приведенную стоимость в нулевой момент времени и будущую стоимость этих платежей через три года.
| P =? | _ | _ | _ | _ | 2000 | _ | _ | _ | 2000 | _ | _ | _ | 2000 | F =? |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||
Квартальная процентная ставка i = 12/4 = 3%
P = 2,000 * (P / F3%, 4) + 2,000 * (P / F3%, 8) + 2,000 * (P / F3%, 12) = 2000 [1 / (1 + 0.03) 4] +2000 [(1 + 1 / 0,03) 8] +2000 [1 / (1 + 0,03) 12] = 4 758,55 долл. США
F = 2 000 * (F / P3%, (12−4)) + 2 000 * (F / P3%, (12-8)) + 2,000 * (F / P3%, (12-12)) = 2,000 * (F / P3%, 8) + 2000 * (F / P3%, 4) + 2000 = 2000 * (1 + 0,03) 8 + 2000 * (1 + 0,03) 4+ 2000 = 6 784,56 долларов США
Обратите внимание, , что, поскольку процентная ставка начисляется ежеквартально, мы должны структурировать расчеты на квартальной основе. Таким образом, на временной шкале будет 12 кварталов (три года и 4 квартала в год).
Проценты в размере 2000 долларов выплачиваются в конце первого, второго и третьего года, которые будут последними кварталами каждого года (4 -й квартал , 8 -й квартал и 12 -й квартал ). ).
Посмотрите следующее видео, Пример номинальной и периодической процентной ставки (время 3:45).
Номинальные и периодические процентные ставки
Щелкните, чтобы просмотреть стенограмму видеоролика «Пример номинальных и периодических процентных ставок».
ВЕДУЩИЙ: Давайте поработаем на примере. Предположим, есть инвестиция, которая приносит вам 2000 долларов в конце первого, второго и третьего года при годовой процентной ставке 12%, начисляемой ежеквартально.И мы хотим рассчитать текущую стоимость в нулевой момент времени и будущую стоимость в конце третьего года этих платежей.
Первое, что нам нужно сделать, это нарисовать временную шкалу и найти платежи на ней. Наименьший интервал на временной шкале должен быть периодом начисления сложных процентов, который в данном примере равен кварталу. Срок эксплуатации проекта — три года. Итак, у нас должно быть 12 кварталов или временной интервал на временной шкале.
Затем размещаем выплаты. Первый платеж в конце года, то есть в 4 квартале.Второй платеж в размере 2000 долларов будет произведен в конце второго года, то есть в 8-м квартале. И третий платеж в конце третьего года, то есть в двенадцатом квартале.
Теперь нам нужно рассчитать приведенную стоимость этих платежей. Но сначала нам нужно рассчитать процентную ставку за период, которая будет равна 12, разделенному на 4, и будет равно 3, потому что в году у нас 4 квартала. Очень важно отметить, что мы должны использовать процентную ставку периода, потому что наши временные интервалы являются квартальными.
Затем мы рассчитываем текущую стоимость этих платежей. Первый платеж в конце первого года, который будет 4-м кварталом, с процентной ставкой 3% за квартал. Второй платеж в 8 квартале с процентной ставкой 3% в квартал. И третьи 2000 долларов приходятся на 12 квартал с процентной ставкой 3%. И результат, который показывает текущую стоимость этих трех платежей.
Теперь, будущая стоимость. Опять же, сначала мы должны рассчитать процентную ставку за период, и она будет 3%.Затем мы рассчитываем будущую стоимость этих трех платежей. Под будущей стоимостью мы подразумеваем конец жизненного цикла проекта, то есть конец третьего года или 12-го квартала. Чтобы рассчитать приведенную стоимость первого платежа, нам нужно знать, сколько периодов времени проходит между этим временем и будущим временем.
Первые 2000 долларов выплачиваются в 4-м квартале, что на 8 кварталов от будущего времени, потому что будущее время приходится на 12-й период. Таким образом, нам нужно записать 12 минус 4 как период времени здесь в множителе, потому что будущее время находится в 12-м периоде.Вторые 2000 долларов выплачиваются в конце второго года или 8-го квартала, что на 4 квартала от будущего времени. И последние 2000 долларов выплачиваются в конце третьего года или 12-го периода. Это то же время, что и мы желаем в будущем. И N или разница во времени будет равна нулю.
Кредит: Фарид Тайари
Непрерывное начисление процентов
Если годовая процентная ставка составляет ежегодно, то она должна увеличиваться один раз в год.
Если годовая процентная ставка составляет полугодие, то она должна увеличиваться дважды в год.
Если годовая процентная ставка составляет квартал, то она должна увеличиваться 4 раза в год.
Если годовая процентная ставка составляет ежемесячно, то она должна увеличиваться 12 раз в год.
Если годовая процентная ставка усугубляется ежедневно, то она должна увеличиваться 365 раз в год.
И если период начисления становится меньше, то количество начислений в год, м , становится больше. В пределе, когда м уходит в бесконечность, процент периода и приближается к нулю.Этот случай называется «Продолжает усугубление интереса». С помощью дифференциального исчисления можно рассчитать коэффициент сложного размера непрерывных процентов для единичного дискретного платежа ( F / P r, n ) как:
F / Pr, n = ern
(Уравнение 2-3)
И, коэффициент текущей стоимости однократного дискретного платежа по непрерывной процентной ставке ( P / Fr, n )
P / Fr, n = 1 / ern
(Уравнение 2-4)
r — номинальная процентная ставка, непрерывно начисляемая
n — количество дискретных периодов оценки
e — натуральный логарифм (ln) = 2.7183
Пример 2-2:
Давайте пересчитаем пример 2-1 с учетом продолжающейся сложной процентной ставки 12%:
P = 2,000 * (P / F12%, 1) + 2,000 * (P / F12%, 2) + 2,000 * (P / F12%, 3) = 2000 [1 / e0,12 * 1] +2000 [1 / e0,12 * 2] +2000 [1 / e0,12 * 3] = 4742,45 долл. СШАF = 2,000 * (F / P12%, 2) + 2,000 * (F / P12%, 1) + 2,000 = 2000 * e0,12 * 2 + 2000 * e0,12 * 1 + 2000 = 6 797,49 долл. США
Примечание: Следующие ссылки объясняют, как использовать функцию Excel (EXP) для вычисления e в степени числа:
Ссылка 1: Функция EXP в Excel
Ссылка 2: Функции Excel
Пожалуйста, посмотрите следующее видео, Непрерывное сложение процентов (время 4:54).
Непрерывное начисление процентов
Щелкните, чтобы увидеть стенограмму видео «Непрерывное усугубление интереса».
В этом видео я собираюсь объяснить непрерывное начисление сложных процентов и покажу вам, как рассчитать будущую и настоящую стоимость в случае непрерывного начисления процентов.
Если у нас в году все больше и больше периода начисления сложных процентов, то период начисления процентов становится все меньше и меньше. Тогда количество периодов начисления сложных процентов в году m становится все больше и больше.Таким образом, в этом случае будущая стоимость может быть рассчитана как настоящее время: умножьте 1 плюс i, степень n, умножьте m. M — количество периодов начисления сложных процентов в год. I — периодическая процентная ставка, равная r, деленному на m, а r — номинальная процентная ставка, которая равна m, умноженному на i.
В пределе, когда m стремится к бесконечности, периодическая процентная ставка i, которая равна r, деленному на m, приближается к 0. В этом случае это называется непрерывным начислением процентов.
Теперь давайте вычислим коэффициент сложного количества, F над P, или коэффициент будущей стоимости для непрерывных процентов.Таким образом, этот множитель равен 1 плюс i в степени n, умноженной на m, и мы можем переписать i как r вместо m.
Теперь нам нужно вычислить предел, когда m стремится к бесконечности. В этом случае этот член приближается к 0, а этот член стремится к бесконечности. Таким образом, мы можем извлечь здесь член e и вычислить предел как e power rn.
Таким образом, коэффициент сложного количества или коэффициент будущей стоимости для непрерывных процентов будет равен e power rn, или будущая стоимость может быть рассчитана как P умножить на e power rn. F — будущая стоимость непрерывного начисления сложных процентов.R — номинальная процентная ставка, начисляемая непрерывно, n — количество дискретных периодов оценки, которые могут составлять один год, два года, три года и т. Д. А е — основа натурального бревна.
Аналогичным образом мы можем рассчитать текущую стоимость в случае непрерывного начисления сложных процентов. Коэффициент текущей стоимости равен коэффициенту, обратному коэффициенту будущей стоимости. Таким образом, приведенная стоимость может быть рассчитана как P равно F, деленному на e степень r, n. P — это текущая стоимость непрерывного начисления процентов.
А теперь поработаем на примере.Это предыдущий пример, но мы собираемся рассмотреть процентную ставку непрерывного начисления сложных процентов. Предположим, есть инвестиция, которая приносит вам 2000 долларов в конце первого, второго и третьего года, и вы хотите рассчитать приведенную стоимость в настоящее время и будущую стоимость в конце третьего года. И мы должны учитывать постоянную процентную ставку по начислению сложных процентов в размере 12%.
Сначала мы рисуем временную шкалу. У нас будет три платежа по 2000 долларов в конце первого, второго и третьего года, и мы хотим рассчитать приведенную стоимость этих трех платежей.
Первый платеж будет в конце первого года. Таким образом, нам нужно дисконтировать это за один год с 12% непрерывной процентной ставки. Второй платеж будет в конце второго года, поэтому n будет 2. И последний платеж будет в третьем году, поэтому n равно 3.
А теперь подставляем множитель, который будет равен 1 на степень 12%, умноженную на 1 и так далее, и результат.
Теперь мы собираемся рассчитать будущую стоимость этих трех платежей.Первый платеж происходит в конце первого года, то есть через два года от будущего времени. Таким образом, n равно 2. Второй платеж находится на расстоянии одного года от будущего времени, поэтому n равно 1. И последний платеж происходит точно в то же время, что и будущее время, поэтому n равно 0, и мы записываем 2000 долларов, а не не нужны никакие компаунды. А затем заменяем факторы. E мощность 12% умножьте на 2 для первого платежа и так далее. И у нас есть результат.
Кредит: Фарид Тайари
«Фиксированная» или «Дополнительная» процентная ставка
Фиксированная или дополнительная процентная ставка применяется к основной сумме первоначальных инвестиций в каждый период начисления процентов .Это означает, что общий процент, полученный за инвестиции по фиксированной процентной ставке, рассчитывается линейно и представляет собой просто сумму процентов за все периоды. Например, если вы инвестируете 1000 долларов в настоящее время в проект с фиксированной процентной ставкой 12% годовых на 100 дней, то через 100 дней вы получите 32,88 доллара:
1000 * 0,12 * (100/365) = 32,88 доллара. Проценты
Фиксированная процентная ставка обычно применяется, когда проценты начисляются за часть года или периода.
Примечание. В инженерной экономике термин «простой процент» обычно используется как «дополнительная» или «фиксированная» процентная ставка, как определено здесь.
Как рассчитать процентную ставку по банковским кредитам
Прежде чем брать ссуду в банке, вам необходимо знать, как рассчитывается ваша процентная ставка, и понимать, как рассчитывать ее самостоятельно.
Банки используют различные методы для расчета процентных ставок, и каждый из них изменяет размер выплачиваемых вами процентов. Если вы знаете, как рассчитывать процентные ставки, вы лучше поймете свой кредитный договор с вашим банком. Вы также сможете лучше согласовать процентную ставку.
Когда банк назначает вам процентную ставку, он указывает так называемую эффективную процентную ставку, также известную как годовая процентная ставка (APR). Годовая процентная ставка отличается от заявленной процентной ставки из-за эффекта начисления процентов.
Банки также могут привязать вашу процентную ставку к ориентиру, обычно это основная процентная ставка. Если ваш заем включает такой резерв, ваша процентная ставка будет варьироваться в зависимости от колебаний этого ориентира.
Расчет процентов по годовой ссуде
Если вы занимаете 1000 долларов в банке на один год и должны платить 60 долларов процентов за этот год, ваша заявленная процентная ставка составляет 6%.Вот расчет:
Эффективная ставка по простой процентной ссуде = проценты / основная сумма = 60 долларов / 1000 долларов = 6%
Ваша годовая процентная ставка или годовая процентная ставка такая же, как указанная в этом примере, потому что здесь нет сложных процентов, которые следует учитывать. Это простая ссуда под проценты.
Между тем, этот конкретный кредит становится менее выгодным, если вы храните деньги в течение более короткого периода времени. Например, если вы занимаетесь 1000 долларов в банке на 120 дней, а процентная ставка остается на уровне 6%, эффективная годовая процентная ставка будет намного выше.
Эффективная ставка = проценты / основная сумма X дней в году (360) / дней выдачи кредита
Эффективная ставка по кредиту на срок менее одного года = 60 долларов США / 1000 долларов США X 360/120 = 18%
Эффективная процентная ставка составляет 18%, так как вы можете использовать средства только в течение 120 дней вместо 360 дней.
Эффективная процентная ставка по дисконтированной ссуде
Некоторые банки предлагают кредиты со скидкой. Ссуды со скидкой — это ссуды, по которым процентные платежи вычитаются из основной суммы до выплаты ссуды.
Эффективная ставка по дисконтированной ссуде = [Процентная ставка X дней в году (360) / Количество дней ссуды неоплачено] / [Основная сумма — Проценты]
Эффективная ставка по дисконтированной ссуде = (60 X 360/360) / (1000 — 60 долларов США) = 6,38%
Как видите, эффективная процентная ставка по льготной ссуде выше, чем по простой процентной ссуде.
Эффективная процентная ставка с компенсационным остатком
Некоторые банки требуют, чтобы малый бизнес, подающий заявку на ссуду коммерческого банка, держал баланс, называемый компенсационным балансом, в их банке, прежде чем они одобрит ссуду.Это требование повышает эффективную процентную ставку.
Эффективная ставка с компенсационным остатком (c) = Проценты / (1-c)
Компенсирующий баланс эффективной ставки = 6% / (1 — 0,2) = 7,5 процента (если c — 20-процентный компенсационный баланс)
Эффективная процентная ставка по ссудам с рассрочкой платежа
Многие потребители имеют ссуды в рассрочку, то есть ссуды, которые погашаются определенным количеством платежей. Например, большинство автокредитов — это ссуды в рассрочку.
К сожалению, одна из самых запутанных процентных ставок по банковской ссуде — это процентная ставка по ссуде в рассрочку. Процентные ставки по кредиту в рассрочку, как правило, являются самыми высокими процентными ставками, с которыми вы столкнетесь. Используя приведенный выше пример:
Эффективная ставка по кредиту в рассрочку = 2 X Годовое количество платежей X Проценты / (Общее количество платежей + 1) X Основная сумма
Эффективная ставка / кредит в рассрочку = (2 X 12 X 60 долларов США) / (13 X 1000 долларов США) = 11,08%
Процентная ставка по кредиту в рассрочку — 11.08% по сравнению с 7,5% по кредиту с компенсационными остатками.
Формула эффективной процентной ставки
— что это такое?
Эффективная годовая процентная ставка (EAR) — это годовая процентная ставка, полученная от любых инвестиций / сбережений, по которым выплачиваются проценты, после того, как она была скорректирована для соответствующего начисления сложных процентов. Если вы не знаете, сложный или сложный процент — это процесс, при котором основная инвестированная сумма со временем увеличивается по мере того, как к нему добавляются накопленные проценты.Например, если вы инвестируете RS. 1000 рупий сегодня, которые увеличиваются ежегодно, у вас были бы рупии. 50 процентов до конца года. Затем это будет добавлено к вашему основному капиталу, увеличив его до рупий. 1050 на следующий год. Затем цикл повторяется. Как видите, ваши накопленные проценты за следующий год будут выше, чем в предыдущие годы, потому что ваша основная сумма также выросла. Это имеет тенденцию увеличиваться со временем как снежный ком и приводит к экспоненциальному росту.
Банки, рекламируя свои услуги, часто рекламируют свою номинальную процентную ставку, например, для сберегательного счета.Однако именно эффективная процентная ставка, рекламируемая вместе с номинальной процентной ставкой, является более точным представлением реальной доходности. Кроме того, эффективная годовая процентная ставка также отражает любые требуемые дополнительные сборы и т. Д.
Расчет эффективной годовой процентной ставки
Эффективную годовую процентную ставку для любого инвестиционного или сберегательного счета можно использовать, используя следующую формулу эффективной годовой процентной ставки:
Эффективная годовая процентная ставка = (1 + i / n) ^ n -1.
- «i» представляет номинальную процентную ставку
- «n» отражает период времени или количество периодов.
Рассмотрим пример.
Допустим, физическое лицо вкладывает 10 000 рупий на свой сберегательный счет под годовую процентную ставку 12%, которая начисляется ежемесячно.
Может показаться, что к концу года у вас будет рупий. 1200 процентов. Однако, если выполнить расчет с ежемесячным начислением сложных процентов, вы увидите, что вы получаете накопленные проценты в размере рупий.12–1
Это будет равно 0,1268 или 12,7% годовых при округлении.
Таким образом, хотя номинальная процентная ставка изначально составляла 12%, применение формулы эффективной годовой процентной ставки помогло нам определить эффективную процентную ставку или вашу фактическую ставку доходности, которая на 0,7% выше номинальной.
Эту формулу можно использовать в реальном сценарии, например, при выборе сберегательного счета или банка для получения ссуды. Традиционно банки, как правило, в своих сберегательных счетах уделяют больше внимания эффективной годовой процентной ставке и меньше — номинальной ставке, поскольку клиенты чувствуют, что получают более высокие проценты.В качестве альтернативы, при рекламе ссуд рекламируется номинальная процентная ставка, поскольку это создает впечатление более низких процентных выплат для заемщика. В то время как в приведенном выше примере процентная ставка варьируется менее чем на 1%, увеличение периода времени окажет значительное влияние на процентную ставку, и поэтому всегда следует убедиться, что они тщательно проверяют детали и положения процентной ставки, прежде чем выбирать какие-либо данная услуга.
Давайте возьмем другой пример, в котором можно сравнить предложения двух банков по сберегательному счету.12-1, или 11,6%
Теперь клиент лучше знает процентные ставки, которые он реально получит, и может принять более обоснованное решение.
Это также может быть применено к рынку ценных бумаг, где инвесторы, например, хотят инвестировать в облигации. Если определенная облигация предлагает процентную ставку 6% раз в полгода, инвестиции в размере 10 000 дадут инвестору доход в 300 рупий в течение первых 6 месяцев. Во вторых 6 инвестор получит 390.Таким образом, хотя номинальная процентная ставка составляет 6%, применение формулы эффективной процентной ставки показывает, что эффективная процентная ставка фактически составляет 6,9%.
Заключение
Формула эффективной процентной ставки может использоваться для получения основной выгоды от использования эффективной годовой ставки; тот факт, что он предлагает более реальное представление и точную цифру процентной ставки, которую можно было бы получить по инвестиционному, сберегательному счету или любому финансовому инструменту.Эффективная процентная ставка, наиболее часто используемая на рынке облигаций, позволяет инвесторам рассчитывать реальную процентную ставку за определенный период времени на основе фактической стоимости данного инструмента.

 Каждые две недели, с целью поддержать ликвидность в финансовой системе, европейский регулятор проводит тендер по размещению средств. То есть, по сути, это минимальная ставка, по которой проходит совершение сделок ЕЦБ на открытом рынке. Refinancing tender является второй по значимости процентной ставкой в мире.
Каждые две недели, с целью поддержать ликвидность в финансовой системе, европейский регулятор проводит тендер по размещению средств. То есть, по сути, это минимальная ставка, по которой проходит совершение сделок ЕЦБ на открытом рынке. Refinancing tender является второй по значимости процентной ставкой в мире.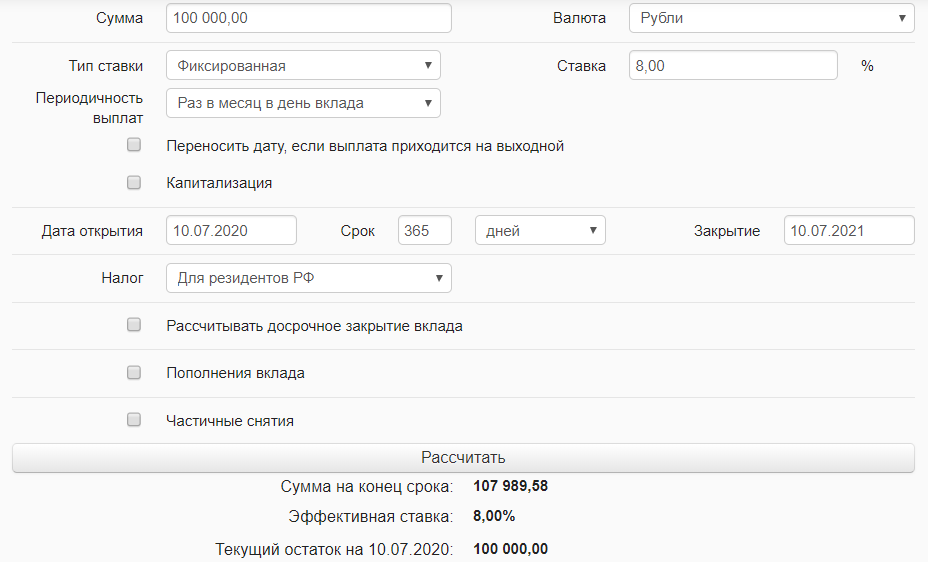 Является аналогом американской Target Fed Fund Rate. Процентная ставка Банка Японии является для него ориентиром в качестве среднего значения на рынке краткосрочных вкладов. Чтобы приблизить процентные ставки по банковским депозитам к целевому значению, Банк Японии манипулирует государственными ценными бумагами.
Является аналогом американской Target Fed Fund Rate. Процентная ставка Банка Японии является для него ориентиром в качестве среднего значения на рынке краткосрочных вкладов. Чтобы приблизить процентные ставки по банковским депозитам к целевому значению, Банк Японии манипулирует государственными ценными бумагами.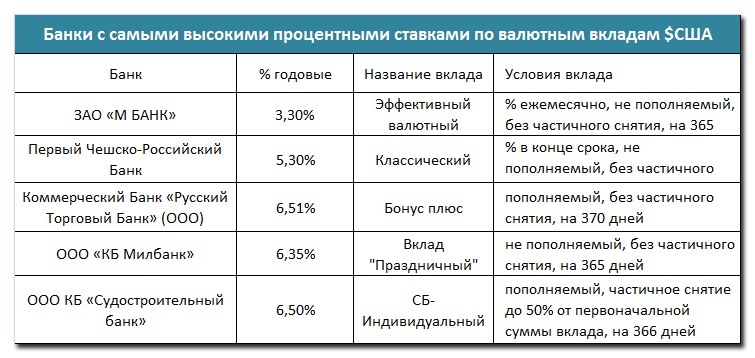 Регулятор принимает от коммерческих банков средства на депозит с процентной ставкой на 0,25% меньше официальной и дает кредит со ставкой на 0,25% больше официальной.
Регулятор принимает от коммерческих банков средства на депозит с процентной ставкой на 0,25% меньше официальной и дает кредит со ставкой на 0,25% больше официальной. В таких соглашениях между двумя сторонами определяется величина ставки;
В таких соглашениях между двумя сторонами определяется величина ставки;
 Базисная точка — одна сотая процента.
Базисная точка — одна сотая процента.